线性回归

线性回归是一种基本的监督学习算法，通过在目标变量和一或多个预测变量之间建立线性关系来预测连续的目标变量。该算法使用线性方程来模拟这种关系，其中预测变量变化会导致目标变量成比例变化。目标是找到最佳拟合线，以最小化预测值和实际值之间平方差的和。

想象一下，你正尝试根据房子的面积来预测其价格。线性回归试图找到一条最能反映这两个变量之间关系的直线。随着房屋面积的增加，价格一般也会增加。线性回归量化了这种关系，使我们能够根据房屋面积预测房屋价格。

什么是回归？

深入了解线性回归之前，有必要先了解机器学习中 回归分析的广泛概念。。回归分析是一种监督学习类型，其目标是预测一个连续的目标变量。这个目标变量可以在给定范围内取任何值。把它想象成估计一个数字，而不是将某物分类到类别中（这正是分类算法所做的事情）。

回归问题的例子包括：

• 根据房屋面积、位置和房龄预测房屋价格。
• 根据历史天气数据预测每日气温。
• 根据营销费用和时间估算网站访客数量。

在所有这些情况下，我们试图预测的输出都是一个连续值。这就是回归与分类的区别所在，分类的输出是一个分类标签（如 "垃圾邮件 "或 "非垃圾邮件"）。

现在，在明确了这一点之后，让我们重温一下线性回归。这只是回归分析的一种特定类型，我们假设预测变量和目标变量之间存在 线性关系。这意味着我们试图用一条直线来模拟这种关系。

简单线性回归

在最简单的形式中，简单线性回归涉及一个预测变量和一个目标变量。一个线性方程表示它们之间的关系：

y = mx + c

Python

• y 是预测的目标变量
• x 是预测变量
• m 是直线的斜率（表示 x 和 y 之间的关系）
• c 是 y-截距（当 x 为 0 时 y 的值）。

简单描述：一元函数

该算法旨在找到 m 和 c 的最佳值，使训练数据中的预测 y 值与实际 y 值之间的误差最小。这通常使用 二进制最小二乘法(OLS) 来实现，其目的是最小化平方误差之和。

多元线性回归

如果涉及多个预测变量，则称为 多重线性回归。方程变为

y = b0 + b1x1 + b2x2 + ... + bnxn

Python

• y 是预测的目标变量
• x1, x2, ..., xn 是预测变量
• b0 为 y-截距
• b1、b2、......、bn 是代表各预测变量与目标变量之间关系的系数。

简单描述：多元函数

普通最小二乘法

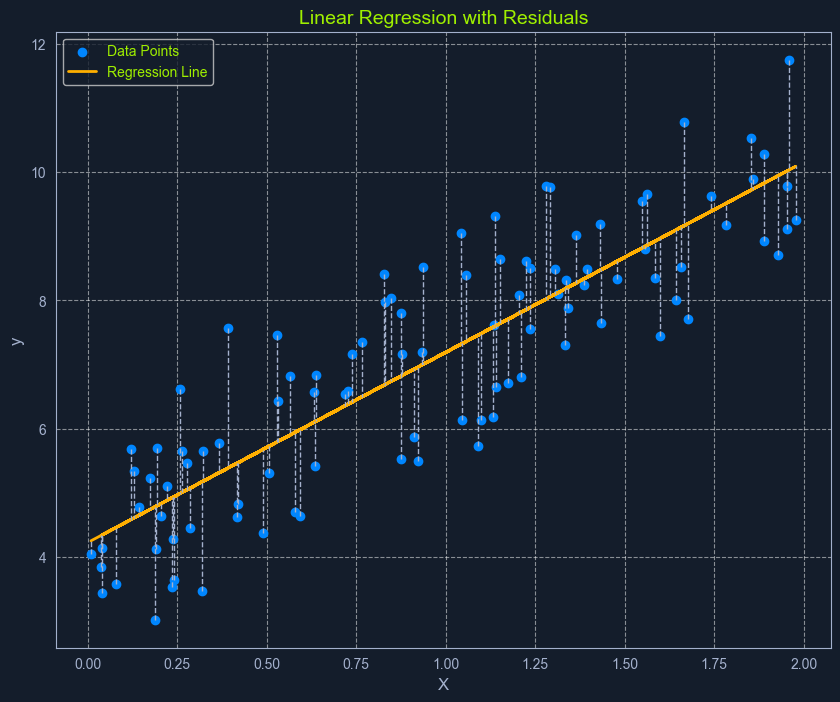
普通最小二乘法（OLS）是估计线性回归中系数最优值的常用方法。它的目的是最小化实际值与模型预测值之间的平方差之和。

把它想象成找到一条能使数据点与直线之间形成的正方形总面积最小的直线。这条 "最佳拟合线 "代表了最能描述数据的关系。

下面是 OLS 过程的详细内容：

1. 计算残差：对于每个数据点，残差是实际y值与模型预测的y值之间的差值。
2. 对残差进行平方处理： 对每个残差进行平方处理，以确保所有值均为正值，并对较大误差给予更多权重。
3. 残差平方和： 将所有残差平方和相加，得到一个代表模型总体误差的值。这个和称为 残差平方和（RSS）。
4. 最小化平方残差和：算法会调整系数，以找到使平方残差和（RSS）最小的值。

这个过程可以形象地理解为找到一条能使数据点与直线之间形成的正方形总面积最小的直线。

线性回归假设

线性回归依赖于对数据的几个关键假设：

• 线性： 预测变量和目标变量之间存在线性关系。
• 独立性： 数据集中的观测值是相互独立的。
• 同方差： 误差的方差在预测变量的所有水平上都是恒定的。这意味着在预测值范围内，残差的分布应该大致相同。
• 正态性： 误差呈正态分布。这一假设对于有效推断模型系数非常重要。

在应用线性回归之前评估这些假设可确保模型的有效性和可靠性。如果违反这些假设，模型的预测可能不准确或具有误导性。